Kun ortotrooppisten kerrosten käyttäytyminen mielivaltaisessa koordinaatistossa tunnetaan, on suhteellisen helppoa luoda mekaaninen malli kerroksista koostetulle laminaatille. Käyttöön vakiintunutta laminaattien laskentamallia kutsutaan klassiseksi laminaattiteoriaksi (Classical Lamination Theory, CLT). Se perustana ovat seuraavat oletukset:

• laminaatin muodostavat kerrokset ovat makroskooppisesti homogeenisia eli ominaisuudet ovat samanlaiset kaikissa kerroksen pisteissä
• kerrokset käyttäytyvät lineaariselastisesti
• kerrokset ovat täydellisesti toisiinsa kiinnittyneet eli eivät pääse liukumaan toisiinsa nähden
• laminaatti on tasojännitystilassa
• laminaatin käyttäytyminen on teknisen taivutusteorian mukaista
• laminaatin muodonmuutokset ovat pieniä.

8.3.1 Laminaatin muodonmuutokset

Teknisen taivutusteorian mukainen käyttäytyminen tarkoittaa, että laminaatin keskitason normaalien oletetaan kuormituksessa säilyvän suorina ja olevan aina kohtisuorassa keskitasoa vastaan. Oletusta havainnollistaa kuvassa 8.8 esitetty laminaattipalkin (-laatan) muodonmuutos. Sen mukaisesti laminaatin minkä tahansa pisteen C siirtymän määrittelevät samaan poikkitasoon kuuluvan keskitason pisteen B tasosiirtymät, poikkitason kiertymä ja tarkastelupisteen etäisyys keskitasosta. Poikkitason kiertymän taas määrittelevät pisteen B pystysiirtymän eli keskitason taipuman ensimmäiset derivaatat.

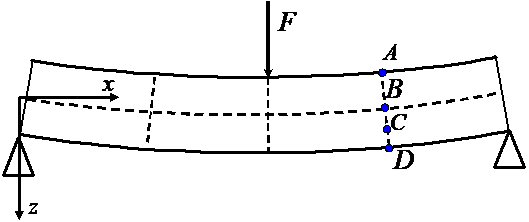
Kuva 8.8 Palkin (laatan) teknisen taivutusteorian mukainen muodonmuutos.

Merkitsemällä kuvan 8.8 pisteen B x-, y– ja z-koordinaatin suuntaisia siirtymiä u₀:lla, v₀:lla ja w₀:lla, voidaan pisteen C tasosiirtymät esittää muodossa:

                                                                                                    (8.42)

Toisaalta, kun siirtymät ovat pieniä, tasovenymien ja siirtymäderivaattojen välillä on yhteys:

                                                                               (8.43)

Sijoittamalla kaava (8.42) kaavaan (8.43) saadaan pisteen C tasovenymille lausekkeet:

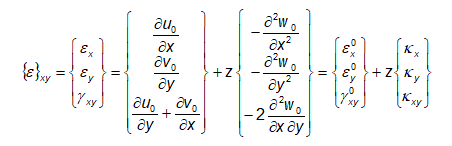
                        (8.44)

joka usein esitetään lyhyesti muodossa

                                                                                           (8.45)

missä venymäkomponenttien ja venymävektorin yläindeksi 0 viittaa laminaatin keskitasoon. Suureiden k_x, k_y ja k_xy yksikkö on rad/m ja niitä kutsutaan käyristymymiksi. Käyristymä on samalla taivutus-/vääntösäteen käänteisluku. Merkitsemällä säteitä R_x:llä, R_y:llä ja R_xy:llä, voidaan kirjoittaa:

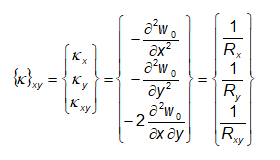
                                                                  (8.46)

Toisaalta luvussa 2 todettiin, että laminaatin venymät yhdistetyssä taso- ja taivutuskuormituksessa voidaan tehdyin oletuksin esittää muodossa:

                                                                                      (8.47)

missä yläindeksi f viittaa taivutusvenymiin (vrt. kuva 2.14). Vertaamalla lausekkeita (8.45) ja (8.47) todetaan käyristymien ja taivutusvenymien välillä oleva yhteys:

                                                                                                       (8.48)

8.3.2 Symmetrinen laminaatti tasokuormituksessa

Kun keskitasonsa suhteen symmetristä laminaattia kuormitetaan tasossa normaalivoimilla ja leikkausvoimalla, kaikkien kerrosten venymät (e_x, e_y ja g_xy) ovat yhtä suuret (kuva 8.9a). Erilaisista materiaaleista valmistetuilla ja eri tavoin suunnatuilla kerroksilla on kuitenkin erilaiset jäykkyydet, minkä seurauksena kerrosjännitykset vaihtelevat. Koska kerrokset oletetaan makroskooppisesti homogeenisiksi, jännitystila on kuvan 8.9b mukainen eli jännitys on vakio kerroksen alueella ja muuttuu hyppäyksellä kahden eri tavoin käyttäytyvän kerroksen rajapinnassa.

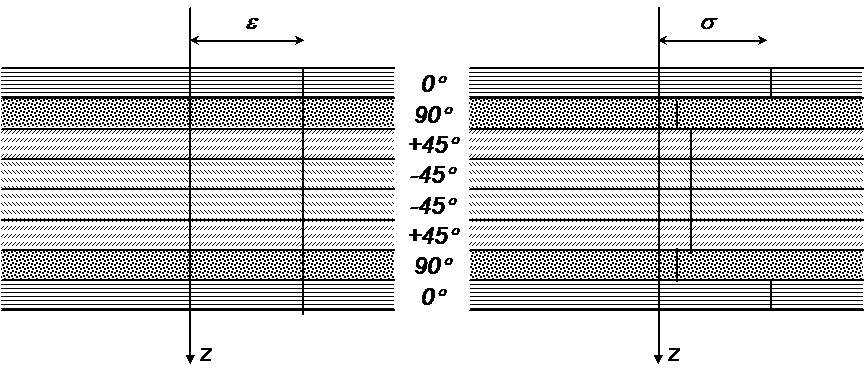
Kuva 8.9 Symmetrisen laminaatin venymät ja jännitykset tasokuormituksessa.

Luvun 2 mukaisesti laminaattiin kohdistuva mekaaninen kuorma kuvataan tavallisesti voimina leveysyksikköä kohti. Kerrosjännitykset ovat näiden voimien aiheuttamia. Voimat ovat kerrosjännitysten resultantteja, joten voimien ja jännitysten välillä on yhteys

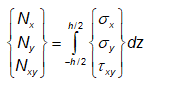
                                                                                            (8.49)

joka voidaan esittää lyhyemmin muodossa

                                                                                                 (8.50)

Ottamalla edelleen huomioon kerroksen jännityksille ja venymille johdettu yhteys (8.33), saadaan edellisestä

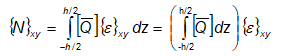
                                                             (8.51)

missä integraalin sisällä oleva matriisi on tarkastelupisteen sisältävän kerroksen jäykkyysmatriisi laminaattikoordinaatistossa. Kaavan jälkimmäinen muoto on saatu siirtämällä koko laminaatin alueella vakioiksi todetut venymät integraalin ulkopuolelle. Koska kerrokset oletettiin myös homogeenisiksi, lausekkeen (8.51) integraali voidaan korvata summauksella:

                                                                     (8.52)

missä n on laminaatin kerrosten lukumäärä ja h_k on kerroksen k paksuus. Lauseke (8.52) kuvaa symmetrisen laminaatin käyttäytymisen tasokuormituksessa. Venymävektorin 3×3 kerroinmatriisi [A] on laminaatin tasojäykkyysmatriisi, jonka alkioiden arvot on laskettavissa, kun laminaatin rakenne ja kerrosominaisuudet tunnetaan:

                                                                      (8.53a,b)

Lausekkeesta (8.52) saadaan edelleen määritettyä tunnetun kuormitustilan aiheuttamat laminaatin venymät. Merkitsemällä [A]:n käänteismatriisia eli laminaatin tasojoustomatriisia [a]:lla saadaan:

                                                                                 (8.54)

Luvun 2 mukaisesti laminaatin kuormitus voidaan kuvata myös keskimääräisillä eli ns. normalisoiduilla jännityksillä, jotka saadaan yksinkertaisesti jakamalla leveysyksikköä kohti ilmoitetut voimat laminaatin paksuudella. Tätä tapaa käyttäen lausekkeet (8.52) ja (8.54) muuntuvat muotoon:

                                                        (8.55a,b)

missä jännityksen yläindeksi 0 viittaa normalisoituun arvoon. Uudet kerroinmatriisit [A^*] ja [a^*] ovat laminaatin normalisoidut tasojäykkyys– ja tasojoustomatriisit:

                                                                                                     (8.56 a,b)

Laminaatin kimmoarvot on määritettävissä normalisoidusta tasojoustomatriisista kimmoarvojen määrittelyn mukaisesti. Kappaleen 8.2 kerrostarkasteluja vastaavasti saadaan:

                         (8.57a-i)

Lausekkeiden (8.57) mukaisesti laminaatin käyttäytymisen täydelliseen kuvaamiseen tarvitaan modulien ja Poissonin vakioiden ohella Lekhnitskiin vakiot, jotka ovat nollasta poikkeavia, kun laminaatti on balansoimaton (kts. kpl. 2.4.1). Lisäksi on huomattava, että kimmoarvot eivät määrittele todellisia jännitysvenymäsuhteita vaan laminaatin todellisten venymien ja keskimääräisten eli normalisoitujen jännitysten väliset suhteet.

Kerrossuuntien vaikutusta laminaatin moduleihin on havainnollistettu luvun 6 esimerkeissä (kuvat 6.18 ja 6.19).

Esimerkki

Esimerkkinä tarkastellaan nelikerroksista [+45/-45]SE-laminaattia, joka valmistetaan taulukon 8.1 mukaisesta, 0,5 mm paksuisesta lasikuitu/epoksi-yhdensuuntaiskerroksesta.

Laminaatin +45°-kerrosten jäykkyysmatriisi määritettiin kappaleen 8.2.3 esimerkissä. Vastaavaan tapaan voidaan laskea jäykkyysmatriisi -45°-kerrokselle. Lopputuloksena saadaan:

Laminaatin jäykkyysmatriisiksi saadaan kaavan (8.53) mukaisesti

Tuloksen mukaisesti jäykkyysmatriisin kytkentätermit 16 ja 26 häviävät, koska suuntakulmiltaan vastakkaismerkkisten kerrosten kytkentätermit ovat erimerkkisiä ja itseisarvoltaan samansuuruisia. Aksiaalikuorma ei näin ollen aiheuta laminaattiin leikkausmuodonmuutosta eikä leikkauskuorma normaalivenymiä.

Laminaatin normalisoitu jäykkyysmatriisi saadaan kaavan (8.56) mukaisesti jakamalla jäykkyysmatriisi laminaatin kokonaispaksuudella:

Normalisoitu joustomatriisi on tämän käänteismatriisi:

Laminaatin kimmoarvot saadaan edelleen laskettua joustomatriisin alkioista kaavoilla (8.57):

Kimmomodulien todetaan olevan jonkin verran suuremmat kuin kappaleen 8.2.3 esimerkissä lasketut +45°-kerroksen kimmomodulit. Selvästi enemmän on kuitenkin kasvanut liukumoduli johtuen siitä, että laminaatissa on jäykkiä kuituja kummankin diagonaalin suunnassa (vrt. luku 6).

8.3.3 Symmetrinen laminaatti taivutuksessa

Symmetrisen laminaatin keskitaso on samalla sen neutraalitaso, jossa lineaarisesti paksuussuunnassa muuttuvat tasovenymät vaihtavat merkkiä, kun laminaattia kuormitetaan puhtaalla taivutuksella (kuva 8.10a). Tasojännitykset muuttuvat homogeenisiksi oletetuissa kerroksissa lineaarisesti, mutta ovat epäjatkuvia eri tavoin käyttäytyvien kerrosten rajapinnoissa (kuva 8.10b)

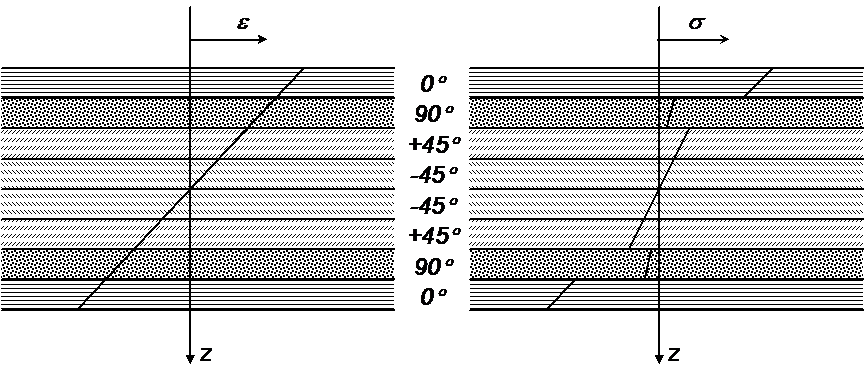
Kuva 8.10 Symmetrisen laminaatin tasovenymät ja -jännitykset taivutuksessa.

Laminaattiin kohdistuva kuorma kuvataan tavallisesti momentteina leveysyksikköä kohti (vrt. luku 2). Kerrosjännitykset ovat momenttien aiheuttamia ja vastaavat momenttivaikutukseltaan laminaattia kuormittavia momentteja. Momenttien ja jännitysten välillä on näin yhteys:

                                                                                         (8.58)

Tämä voidaan esittää lyhyemmin muodossa

                                                                                              (8.59)

Ottamalla huomioon kerroksen jännityksille ja venymille johdettu yhteys vastaavaan tapaan kuin tasokuormitustarkastelussa, saadaan edellisestä

                                                                                        (8.60)

Lausekkeen (8.45) mukaisesti symmetrisen laminaatin puhtaassa taivutuksessa tasovenymien ja laminaatin käyristymien välillä on yhteys

                                                                                                         (8.61)

Kun tämä sijoitetaan lausekkeeseen (8.60) ja siirretään z-koordinaatista riippumattomat laminaatin käyristymät integraalin ulkopuolelle, saadaan momenttien ja laminaatin muodonmuutostilan kuvaavien käyristymien välille yhteys:

                                                                (8.62)

Tämä lauseke kuvaa symmetrisen laminaatin käyttäytymisen puhtaassa taivutuksessa. Käyristymävektorin 3×3 kerroinmatriisi on laminaatin taivutusjäykkyysmatriisi, jonka alkioiden arvot on laskettavissa, kun laminaatin rakenne ja kerrosominaisuudet tunnetaan. Koska kerrokset oletettiin homogeenisiksi, alkioiden arvot voidaan integroinnin sijaan laskea summaamalla:

                              (8.63a,b)

Lausekkeesta (8.62) saadaan edelleen määritettyä tunnetun kuormitustilan aiheuttamat laminaatin käyristymät. Merkitsemällä [D]:n käänteismatriisia eli laminaatin taivutusjoustomatriisia [d]:llä saadaan:

                                                                                (8.64)

Momenttien ja käyristymien sijaan laminaattien taivutuskäyttäytyminen voidaan kuvata myös normalisoitujen taivutusjännitysten ja taivutusvenymien välisillä yhteyksillä. Ottamalla huomioon lausekkeen (2.12) mukainen normalisoitujen taivutusjännitysten ja taivutusmomenttien välinen yhteys sekä lausekkeen (8.48) mukainen taivutusvenymien ja käyristymien välinen yhteys, saadaan lausekkeita (8.62) ja (8.64) vastaten:

                          (8.65 a,b)

missä yläindeksi f viittaa taivutusjännityksen normalisoituun arvoon ja taivutusvenymään eli laminaatin pintavenymään. Uudet kerroinmatriisit [D^*] ja [d^*] ovat laminaatin normalisoidut taivutusjäykkyys– ja taivutusjoustomatriisit:

                                                                                                   (8.66 a,b)

Laminaatin kimmoarvot taivutuksessa voidaan määrittää normalisoidusta taivutusjoustomatriisista vastaavasti kuin tasokimmoarvot tasojoustomatriisista. Viittaamalla taivutuskimmoarvoihin yläindeksillä f saadaan:

                        (8.67a-i)

Tässäkin tapauksessa on huomattava, että kimmoarvot eivät määrittele todellisia jännitysvenymäsuhteita vaan laminaatin todellisten pintavenymien ja normalisoitujen taivutusjännitysten väliset suhteet. Yleisessä tapauksessa jäykkyysmatriisin kaikki alkiot ja sen seurauksena Lekhnitskiin vakiot ovat myös nollasta poikkeavia. Näin taivutusmomentti aikaansaa laminaattiin taipumien ohella vääntymää ja vääntömomentti vääntymän ohella taipumia.

Esimerkki

Edellisen kappaleen esimerkissä määritettiin lasikuitu/epoksi-yhdensuuntaiskerroksesta valmistetun [+45/-45]SE-laminaatin kerroksille jäykkyysmatriisit xy-koordinaatistossa:

Näistä saadaan edelleen laskettua laminaatin taivutusjäykkyysmatriisi kaavaa (8.63) käyttäen. Koska laminaatti on symmetrinen, laskentaa voidaan yksinkertaistaa soveltamalla kaavaa vain laminaatin puolikkaaseen ja kertomalla lopputulos kahdella:

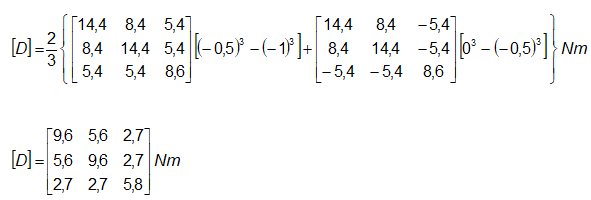
Tästä voidaan edelleen laskea normalisoitu taivutusjäykkyysmatriisi:

Normalisoitu taivutusjoustomatriisi on tämän käänteismatriisi:

 Tämän alkioista saadaan lopuksi laminaatin taivutuskimmoarvoiksi:

Kimmomodulien ja Poissonin vakion todetaan olevan likimain samansuuruiset kuin kappaleessa 8.3.2 lasketut tasokimmoarvot. Näin ei ole kuitenkaan aina. Toisentyyppisellä laminaatilla arvot voisivat erota hyvinkin paljon toisistaan, koska taivutusjäykkyyteen vaikuttaa oleellisesti myös kerrosten pinoamisjärjestys. Huomattavaa on lisäksi, että esimerkkilaminaatin tasojäykkyysmatriisissa kytkentätermit 16 ja 26 hävisivät. Taivutusjäykkyysmatriisissa ne ovat kuitenkin nollasta poikkeavia.

8.3.4 Taso- ja taivutuskuormitettu symmetrinen laminaatti

Symmetristen laminaattien venymät yhdistetyssä taso- ja taivutuskuormituksessa voidaan aina määrittää superponoimalla eli laskemalla taso- ja taivutuskuormien aiheuttamat venymät erikseen ja lopuksi summaamalla ne. Vastaavasti voidaan tietysti määrittää pakkomuodonmuutostilaa vastaavat laminaatin kuormitukset. Superponointi ei kuitenkaan ole mahdollista, mikäli laminaatti on epäsymmetrinen. Tällöin on sovellettava seuraavassa kappaleessa esitettyjä laskentamenetelmiä.

8.3.5 Epäsymmetrinen laminaatti

Keskitasonsa suhteen epäsymmetristen laminaattien käyttäytyminen on huomattavasti monimut­kaisempaa kuin symmetristen. Epäsymmetrisyyden johdosta laminaatin neutraalitaso ei enää yhdy sen geometriseen keskitasoon. Tämän seurauksena laminaatin tasossa vaikuttavat kuormat aiheuttavat normaalivenymien ja mahdollisen liukuman ohella myös laminaatin käyristymistä. Vastaavasti taivutus aiheuttaa paitsi käyristymistä myös normaalivenymiä ja liukumia laminaatin geometrisessa keskitasossa. Tehdyn oletuksen mukaisesti venymät ja liukuma muuttuvat kuitenkin lineaarisesti laminaatin paksuussuunnassa. Venymä- ja jännitysjakautumien yleistä muotoa havainnollistaa kuva 8.11.

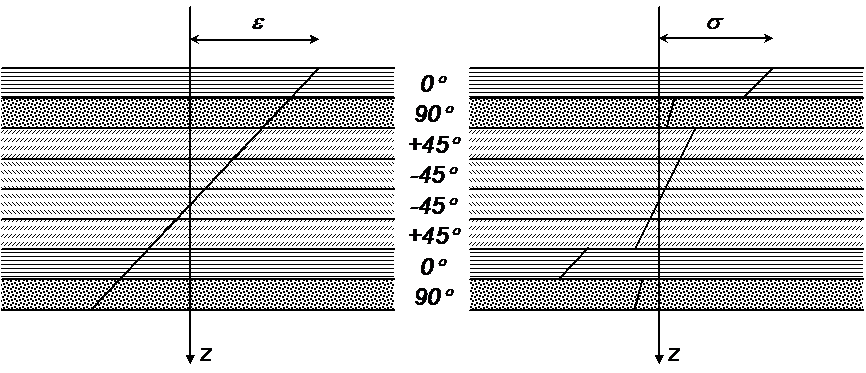
Kuva 8.11 Epäsymmetrisen laminaatin venymät ja jännitykset taivutuksessa.

Epäsymmetristen laminaattien tarkasteluissa laminaatin muodonmuutostila määritellään geometrisen keskitason venyminä ja käyristyminä. Kokonaisvenymät tietyssä poikkileikkauksen pisteessä ovat kuvaa 8.11 ja kaavaa (8.45) vastaten

missä yläindeksi 0 viittaa keskitason venymiin ja z on tarkastelupisteen etäisyys geometrisesta keskitasosta.

Laminaatin käyttäytymismalli voidaan johtaa vastaavaan tapaan kuin symmetrisille laminaateille ulkoisten voimien ja momenttien sekä jännitysten aiheuttamien voimien ja momenttien yhtäsuuruusehdoista:

                                                                                        (8.68a,b)

Yleistetyn Hooken lain ja kaavan (8.45) avulla lausekkeet saadaan edelleen muotoon:

                 (8.69a,b)

Saadut lausekkeet osoittavat, että taso- ja taivutuskuormitustapaukset ovat nyt toisiinsa kytkeytyneet kappaleen alussa tehtyjen toteamusten mukaisesti.

Venymävektorin ja käyristymävektorin kerroinmatriisien tarkastelu osoittaa, että keskitason venymävektorin kertojana on ensimmäisessä yhtälössä laminaatin tasojäykkyysmatriisi [A]. Vastaavasti jälkimmäisessä yhtälössä käyristymävektorin kerroinmatriisi on laminaatin taivutusjäykkyysmatriisi [D]. Kolmas kerroinmatriisi, joka esiintyy kummassakin yhtälössä, kuvaa taso- ja taivutuskuormitustapausten kytkeytymisen, mistä syystä sitä kutsutaan kytkentämatriisiksi:

                                                                                                    (8.70)

Kytkentämatriisin alkiot voidaan laskea vastaavasti kuin muiden jäykkyysmatriisien alkiot. Korvaamalla integraali summauksella yli kerrosten saadaan:

                                                            (8.71)

Matriisiyhtälöpari (8.69) voidaan näin esittää lyhyesti muodossa:

                                                                             (8.72a,b)

Yhtälöpari voidaan myös yhdistää yhdeksi matriisiyhtälöksi, jossa kuormitusvektori sisältää sekä taso- että taivutuskuormat. Laminaatin muodonmuutoksen kuvaa vastaavasti keskitason venymät ja käyristymät sisältävä vektori. Tämän 6×6 kerroinmatriisi muodostuu jäykkyysmatriiseista:

                                                                                       (8.73)

Kaavat (8.72) ja (8.73) määrittelevät yleisimmässä tapauksessa laminaatin kuormitusten ja muodonmuutosten väliset yhteydet. Symmetriselle laminaatille kytkentämatriisi [B] = 0, jolloin kaavat supistuvat aikaisemmin tarkastelluiksi kahdeksi erilliseksi, taso- ja taivutuskuormitusta kuvaavaksi matriisiyh­tälöksi.

Matriisiyhtälöparista (8.72) tai yhtälöstä (8.73) voidaan kääntäen ratkaista venymät ja käyristymät kuormitustilan funktiona. Käyttämällä kaavan (8.73) mukaista esitystapaa, saadaan kerroinmatriisin käännön tuloksena

                                                       (8.74)

missä [a], [b] ja [d] ovat epäsymmetrisen laminaatin taso-, kytkentä– ja taivutusjoustomatriisit. Näiden lausekkeet ovat:

                                                 (8.75)

Luonnollisesti nämäkin matriisit suppenevat symmetrisillä laminaateilla aikaisemmin tarkasteltuun muotoon (kytkentämatriisit häviävät, [a] = [A]^-1, [d] = [D]^-1).

Toisinaan on hyödyllistä kääntää kaavojen (8.72) mukainen matriisiyhtälöpari vain osittain ratkaisemalla ensimmäisestä yhtälöstä keskitason venymät ja sijoittamalla saatu tulos jälkimmäiseen yhtälöön. Lopputulokseksi saadaan:

                                              (8.76a,b)

Ratkaisu on käyttökelpoinen, kun analysoitavana on esimerkiksi epäsymmetrisestä laminaatista valmistettu paineastia tai paineistettu ja aksiaali-/vääntökuormitettu putki. Näissä seinämän käyristyminen on rakenteellisesti estetty ({κ}_xy = 0), jolloin ensimmäisestä kaavasta saadaan tasokuormien aiheuttamat seinämän venymät. Toinen kaava ilmoittaa, miten suuret momentit seinämää kuormittavat, kun seinämä ei pääse vapaasti käyristymään.

Kaavojen (8.74) mukaisten joustomatriisien alkioista voitaisiin edelleen määrittää epäsymmetrisen laminaatin kimmoarvot vastaavaan tapaan kuin ne aikaisemmissa kappaleissa johdettiin symmetrisille laminaateille. Samoin voitaisiin määritellä normalisoidut jäykkyys- ja joustomatriisit. Laminaattien monimutkaisen käyttäytymi­sen takia suureiden käyttö on kuitenkin epähavainnollista. Suositeltavaa onkin käyttää edellä esitettyjä lausekkeita ulkoisen kuormituksen aiheuttaman venymätilan määrittämiseen. Laminaatin venymistä saadaan suoraan määritettyä kerrosten venymät ja näistä tarvittaessa kerrosten jännitystila yleistettyä Hooken lakia soveltaen.

Epäsymmetristen laminaattien käyttö ei yleensä ole suositeltavaa, sillä kuormitusten aiheuttamat muodonmuutokset voivat olla yllättäviä. Lisäksi lämpötila- ja kosteusmuutokset aiheuttavat laminaattien käyristymistä. Epäsymmetrisyyttä on pyritty hyödyntämään lähinnä eräissä virtausteknisissä sovellutuksissa optimoimalla käyttökuormien aiheuttamia muodonmuutoksia siten, että rakenne on kaikilla kuormilla virtausteknisesti tehokas.

8.3.6 Laminaattien luokittelu

Edellisten kappaleiden mukaisesti laminaatin mekaanisen käyttäytymisen kuvaavat sen jäykkyysmatriisit [A], [B] ja [D]. Laminaatit voidaan luokitella matriisien ominaisuuksien perusteella, mistä esimerkkinä on luokittelu symmetrisiin ([B] = 0) ja epäsymmetrisiin ([B] ¹ 0) laminaatteihin. Luokittelua voidaan täsmentää tarkastelemalla erikseen kunkin jäykkyysmatriisin alkioita.

Oman pääryhmänsä muodostavat luonnollisesti symmetriset laminaatit, joiden kytkentämatriisi [B] = 0. Näiden luokittelu on esitetty taulukossa 8.2. Yksinkertaisimmin käyttäytyviä ovat nk. erityisesti ortotrooppiset laminaatit, joilla taso- ja taivutusjäykkyysmatriisien kytkentätermit 16 ja 26 häviävät. Esimerkkejä erityisesti ortotrooppisista laminaateista ovat yhdensuuntaislaminaatit ja symmetriset ristiinladotut laminaatit. Myös eräät symmetriset balansoidut laminaatit ovat erityisesti ortotrooppisia. Tällaiset laminaatit on kootusti esitetty mm. lähteessä [6]. Normaalisti kuitenkin symmetrisen balansoidun laminaatin tasojäykkyysmatriisin [A] kytkentätermit häviävät, mutta taivutusjäykkyysmatriisin [D] kytkentätermit ovat nollasta poikkeavia. Yleisimmässä symmetrisessä laminaatissa myös [A]-matriisin vuorovaikutustermit ovat nollasta poikkeavia.

Taulukko 8.2 Symmetristen laminaattien luokittelu.

Tyyppi/Esimerkki	Jäykkyysmatriisit
Erityisesti ortotrooppinen	A16 = A26 = 0
[0/90/0]	[B] = 0
	D16 = D26 = 0
Balansoitu/kulmaladottu	A16 = A26 = 0
[30/-30/-30/30]	[B] = 0
Symmetrinen	[B] = 0
[30/-45/30]

Toisen laminaattien pääryhmän muodostavat keskitasonsa suhteen antisymmetriset laminaatit. Niissä pääsuunnista x ja y poikkeavat kerrokset esiintyvät +q/-q pareina sijaiten symmetrisesti laminaatin keskitasoon nähden. Laminaatit voivat lisäksi sisältää 0°- ja 90°-suuntaisia kerroksia. Kaikille antisymmetrisille laminaateille on ominaista [A]- ja [D]-matriisien kytkentätermien 16 ja 26 häviäminen. Yksinkertaisimmin käyttäytyviä ovat antisymmetriset ristiinladotut laminaatit, joissa 0°- ja 90°-suuntaiset kerrokset esiintyvät pareittain sijaiten symmetrisesti laminaatin keskitasoon nähden. Näillä laminaateilla sekä [A]- että [D]-matriisin diagonaalitermit 11 ja 22 ovat keskenään yhtä suuret. Kytkentämatriisin [B] alkioista vain 11 ja 22 termit ovat nollasta poikkeavia. Ne ovat itseisarvoltaan yhtä suuret mutta erimerkkiset. Antisymmetrisen balansoidun laminaatin [B]-matriisin alkioista nollasta poikkeavia ovat alkiot 16 ja 26. Yleisimmissä antisymmetrisissä laminaateissa [B]-matriisin alkiot 11, 22, 16 ja 26 ovat nollasta poikkeavia kuitenkin niin, että B₂₂ = – B₁₁. Antisymmetristen laminaattien luokittelu on kootusti esitetty taulukossa 8.3.

Taulukko 8.3 Antisymmetristen laminaattien luokittelu.

Tyyppi/Esimerkki	Jäykkyysmatriisit
Ristiinladottu	A16 = A26 = 0 , A11 = A22
[0/0/90/90]	B22 = -B11 , B16 = B26 = B66 = 0
	D16 = D26 = 0 , D11 = D22
Balansoitu/kulmaladottu	A16 = A26 = 0
[30/-30/30/-30]	B11 = B12 = B22 = B66 = 0
	D16 = D26 = 0
Antisymmetrinen	A16 = A26 = 0
	B12 = B66 = 0 , B22 = -B11
	D16 = D26 = 0

Epäsymmetrisistä laminaateista yksinkertaisimmin käyttäytyviä ovat epäsymmetriset ristiinladotut laminaatit, jotka sisältävät vain 0°- ja 90°-suuntaisia kerroksia mielivaltaisessa järjestyksessä. Näillä kaikkien matriisien termit 16 ja 26 häviävät. Epäsymmetrisillä balansoiduilla laminaateilla [A]-matriisin kytkentätermit häviävät muiden matriisien ollessa täysiä. Yleisimmässä tapauksessa kaikki jäykkyysmatriisit ovat täysiä. Luokittelu on kootusti esitetty taulukossa 8.4.

Taulukko 8.4 Epäsymmetristen laminaattien luokittelu.

Tyyppi/Esimerkki	Jäykkyysmatriisit
Ristiinladottu	A16 = A26 = 0
[0/90/0/0]	B16 = B26 = 0
	D16 = D26 = 0
Kulmaladottu/balansoitu	A16 = A26 = 0
[0/-30/30]
Epäsymmetrinen	kaikkien jäykkyysmatriisien
[0/45/-30]	kaikki alkiot ¹ 0

Jäykkyysmatriisien kytkentätermien merkitykset on esitetty kootusti kuvissa 8.12 ja 8.13. Selvyyden vuoksi kuvat osoittavat pelkästään kytkentätermistä johtuvan muodonmuutoksen. Kuvien mukaisesti:

• Tasojäykkyysmatriisin [A] kytkentätermien 16 ja 26 ollessa nollasta poikkeavia normaalikuormat N_x ja N_y aiheuttavat normaalivenymien ohella liukumaa ja leikkauskuorma N_xy liukuman ohella normaalivenymiä (kuva 8.12).
• Taivutusjäykkyysmatriisin [D] kytkentätermien 16 ja 26 ollessa nollasta poikkeavia taivutusmomentit M_x ja M_y aiheuttavat taipumien ohella vääntymää ja vääntömomentti M_xy vääntymän ohella taipumia (kuva 8.12).
• Kun kytkentämatriisin [B] termit 11, 12 ja 22 ovat nollasta poikkevia, normaalikuormat N_x ja N_y aiheuttavat normaalivenymien ohella taipumia ja taivutusmomentit M_x ja M_y taipumien ohella normaalivenymiä (kuva 8.13).
• Kun kytkentämatriisin [B] termi 66 on nollasta poikkeava, leikkauskuorma N_xy aiheuttaa liukuman ohella vääntymää ja vääntömomentti M_xy vääntymän ohella liukumaa (kuva 8.13).
• Kun kytkentämatriisin [B] termit 16 ja 26 ovat nollasta poikkeavia, normaalikuormat N_x ja N_y aiheuttavat normaalivenymien ohella vääntymää ja vääntömomentti M_xy vääntymän ohella normaalivenymiä. Lisäksi leikkauskuorma N_xy aiheuttaa liukuman ohella taipumia ja taivutusmomentit M_x ja M_y taipumien ohella liukumaa (kuva 8.13).

Kuva 8.12 Tasojäykkyysmatriisin [A] ja taivutusjäykkyysmatriisin [D] kytkentätermien aiheuttamat muodonmuutokset.

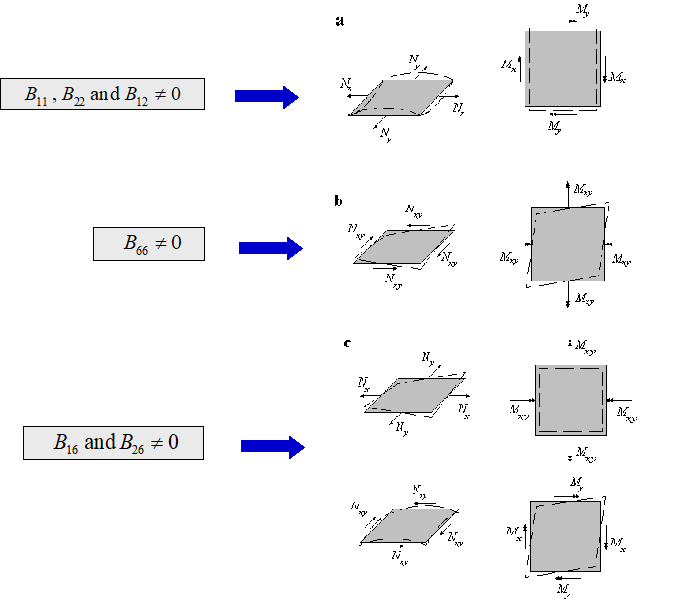
Kuva 8.13 Kytkentämatriisin [B] alkioiden aiheuttamat muodonmuutokset.

8.3.7 Laminaattien lämpö- ja kosteuslaajeneminen

Kuitulujitetun laminaatin lämpö- ja kosteuslaajenemisen arvioimiseksi on tunnettava kerrosten laajenemisominaisuudet niiden pääkoordinaatistossa. Nämä määritetään kokeellisesti tai arvioidaan esisuunnittelua varten sekoituskaavoilla lähtien lujitteen ja muoviaineen laajenemis­kertoimista ja kerroksen lujitepitoisuudesta (vrt. kappale 8.1). Seuraavassa tarkastelussa kerroksen lämpölaajenemiskertoimia pääsuunnissa merkitään a₁:llä ja a₂:lla, kosteuslaajenemiskertoimia vastaavasti β₁:llä ja β₂:lla. Edelliset ilmaisevat yksikön suuruisen lämpötilamuutoksen aiheuttamat venymät kerroksen pääsuunnissa 1 ja 2, jälkimmäiset vastaavasti painoprosenttiyksikön suuruisen kosteuspitoisuuden muutoksen aiheuttamat venymät.

Kerroksen kokonaisvenymät saadaan summaamalla ulkoisen kuorman sekä lämpötila- ja kosteusmuutosten (DT ja Dc) aiheuttamat venymät:

                    (8.77)

Tämä esitetään usein lyhyemmin muodossa

                                                                  (8.78)

missä {a}₁₂ ja {β}₁₂ ovat kerroksen lämpö- ja kosteuslaajenemisvektorit kerroskoordinaatistossa vastaten yksikön suuruista lämpötilan ja kosteuspitoisuuden muutosta.

Kerroksesta muodostetun laminaatin lämpö- ja kosteuslaajenemiskertoimien määrittämiseksi määritellään ekvivalentit lämpö– ja kosteusjännitykset G jännityksinä, jotka aiheuttavat samat muodonmuutokset kuin lämpötila- ja kosteusmuutokset. Määrittelyn mukaisesti ekvivalentit jännitysvektorit ovat kerroskoordinaatistossa:

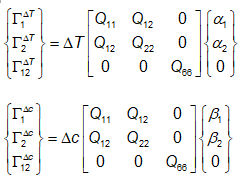
                                                              (8.79a,b)

Yhteydet esitetään seuraavissa tarkasteluissa lyhyemmässä muodossa:

                                                                                      (8.80a,b)

Ekvivalentteihin jännityksiin voidaan soveltaa kappaleessa 8.2 johdettua koordinaatistomuunnosta, jonka mukaisesti kerroksen ekvivalentit lämpö- ja kosteusjännitykset laminaattikoordinaatistossa ovat:

                                                                                      (8.81a,b)

Laminaatille voidaan vastaavasti määritellä ekvivalentit voimat ja momentit, jotka aiheuttavat samat muodonmuutokset kuin laminaatin vapaa lämpö- ja kosteuslaajeneminen. Nämä saadaan summaamalla laminaatin kerrosten ekvivalenttien jännitysten aiheuttamat voimat ja momentit:

                                    (8.82a-d)

Kappaleessa 8.3.5 johdettiin epäsymmetriseen laminaattiin kohdistettujen ulkoisten voimien ja momenttien sekä näiden aiheuttamien keskitason venymien ja käyristymien välille yhteys

Kun laminaatti kokee lämpötila- ja kosteusmuutoksia, osa keskitason venymistä ja käyristymistä johtuu laminaatin vapaista lämpö- ja kosteusmuodonmuutoksista.  Tämä voidaan ottaa huomioon vähentämällä kokonaisvenymien ja -käyristymien määrittelemistä voimista ja momenteista lämpö- ja kosteuslaajenemista vastaavat ekvivalentit voimat ja momentit:

                                                  (8.83)

Tämä voidaan myös esittää muodossa

                                 (8.84)

missä {N^A}_xy on ulkoisten voimien ja ekvivalenttien voimien summa {M^A}_xy:n ollessa vastaavasti ulkoisten momenttien ja ekvivalenttien momenttien summa. Koska ekvivalentit voimat ja momentit eivät todellisuudessa kuormita laminaattia, suureita {N^A}_xy ja {M^A}_xy kutsutaan näennäisiksi voimiksi ja momenteiksi (A = apparent, näennäinen).

Yhtälöstä (8.84) voidaan ratkaista laminaatin venymätila, kun laminaattiin kohdistuu sekä mekaanisia että lämpö- ja kosteuskuormia.

Laminaatin lämpö- ja kosteuslaajenemiskertoimet voidaan määrittää lausekkeesta (8.83) tai (8.84) ottamalla huomioon, että vapaassa laajenemisessa {N}_xy ja {M}_xy häviävät. Kun tarkastellaan pelkkää vapaata lämpölaajenemista, saadaan:

                                                                                   (8.85)

josta edelleen saadaan venymät ja käyristymät ekvivalenttien voimien ja momenttien funktiona:

                                                                                (8.86)

Määritelmän mukaan lämpölaajenemiskertoimet kuvaavat laminaatin vapaan lämpölaajenemisen yhden asteen lämpötilamuutosta vastaten. Epäsymmetrisille laminaateille voidaan vastaavasti määritellä lämpökäyristymiskertoimet, jotka kuvaavat laminaatin vapaan lämpökäyristymisen yhden asteen lämpötilamuutosta vastaten. Kertoimet saadaan sijoittamalla lausekkeeseen (8.86) kaavoilla (8.82a,b) laskettavat ekvivalentit voimat ja momentit yhden asteen suuruista lämpötilamuutosta vastaten. Merkitsemällä vektorimuodossa esitettyjä lämpölaajenemiskertoimia {α}_xy:llä ja lämpökäyristymiskertoimia vastaavasti {δ}_xy:llä saadaan

                                                                               (8.87)

ekvivalenttien voimien ja momenttien yläindeksien osoittaessa, että voimat ja momentit lasketaan yhden asteen lämpötilamuutokselle.

Symmetriselle laminaatille [B] = 0, jolloin lausekkeista (8.87) ja (8.82) saadaan symmetrisen laminaatin lämpölaajenemiskertoimiksi

                                          (8.88)

Symmetrinen laminaatti ei käyristy lämpötilan muuttuessa, kun lämpötilan muutos on sama kaikkialla laminaatissa. Tämä nähdään myös lausekkeesta (8.82b) toteamalla, että symmetriselle laminaatille ekvivalentit momentit häviävät, kun ΔT = vakio.

Epäsymmetriselle laminaatille sekä lämpölaajenemis- että lämpökäyristymiskertoimet ovat nollasta poikkeavia. Kaava (8.88) antaa kuitenkin lämpölaajenemiskertoimet myös epäsymmetriselle laminaatille siinä tapauksessa, että laminaatin käyristyminen on estetty eli {κ}_xy = 0. Tämän osoittaa lauseke (8.76a).

Kosteuslaajenemiskertoimille {β}_xy ja kosteuskäyristymiskertoimille {φ}_xy saadaan analogisesti:

                                                                                (8.89)

Symmetriselle laminaatille kosteuslaajenemiskertoimet ovat kaavaa (8.88) vastaten

                                           (8.90)

8.3.8 Kerrosten venymät ja jännitykset

Kun laminaatin vaste kuormitukseen tunnetaan, voidaan myös tutkia kuorman aiheuttamia venymiä ja jännityksiä kerroksittain. Kerrosten vastetta kuormitukseen havainnollistaa kuvan 8.14 esimerkki, jossa yksinkertaisuuden vuoksi on oletettu, ettei laminaatti käyristy. Kuvan mukaisesti:

• Jännitysvapaa tila on tarkastelun alkutila, jossa laminaatin kerrokset ovat jännityksettömässä tilassa.

• Lämpötila- ja/tai kosteusmuutos aiheuttaa laminaattiin ns. vapaan venymän {e^I}_xy, jonka määrittelevät laminaatin lämpö- ja kosteuslaajenemiskertoimet.

• Laminaatin kokonaisvenymä saadaan lisäämällä lämpö- ja kosteuslaajenemisen aiheuttamiin vapaisiin venymiin ulkoisten kuormien aiheuttamat venymät:

                                  (8.91)

• Yleisessä tapauksessa kerrosten ja laminaatin lämpö- ja kosteuslaajenemiskertoimet ovat erilaiset. Kerroksen vapaa venymä {e₀^I}_xy,k osoittaa, miten se laajenisi, mikäli se ei olisi kiinni muissa kerroksissa. Kerroksen jäännösvenymä {e_r^I}_xy,k on se osa kerroksen vapaata venymää, joka ei pääse syntymään. Kuvan 8.14 mukaisin merkinnöin jäännösvenymä on

                                                                           (8.92)

• Laminaatin kokonaisvenymän ja kerroksen vapaan venymän erotus on ns. ekvivalentti venymä, joka on kerrokseen jännityksiä aiheuttava muodonmuutos:

                                                                           (8.93)

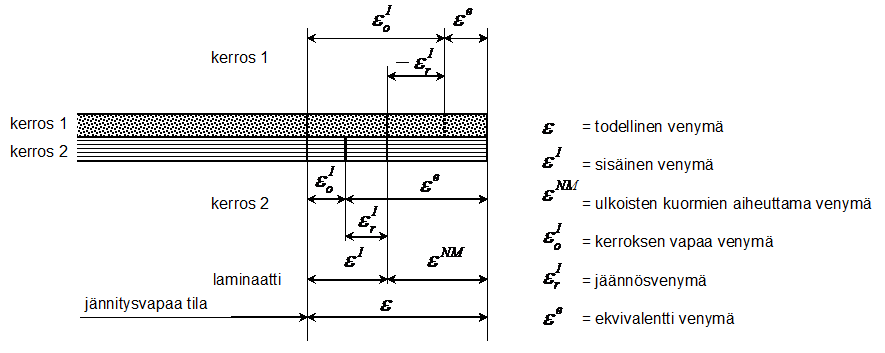
Kuva 8.14 Laminaatin ja sen kerrosten venymät.

Laminaatin muodostavien kerrosten venymä- ja jännitystilat määritetään aina saman proseduurin mukaisesti. Proseduuri on hyvin suoraviivainen ja yksinkertainen, mikäli laminaattiin kohdistuu vain ulkoisia kuormia. Yleisimmässä tapauksessa, kun tarkasteltava laminaatti on epäsymmetrinen, laskenta etenee seuraavasti:

1. Lasketaan laminaatin jäykkyysmatriisit [A], [B] ja [D] kaavoilla (8.53), (8.63) ja (8.71) ja näistä edelleen joustomatriisit [a], [b] ja [d] kaavoilla (8.75).

• Lasketaan kaavalla (8.74) ulkoisten kuormien laminaattiin aiheuttamat keskitason venymät ja käyristymät.

• Lasketaan laminaatin venymistä ja käyristymistä kerrosten venymät laminaattikoordinaatistossa kaavaa (8.45) käyttäen.

• Lasketaan kerroksen laminaattikoordinaatiston venymistä kerroksen venymätila kerroskoordinaatistossa muunnoskaavaa (8.29) käyttäen.

• Lasketaan kerroksen jännitykset kerroskoordinaatistossa kaavalla (8.19).

• Kerrosjännitykset laminaattikoordinaatistossa voidaan tarvittaessa laskea kaavalla (8.31a).

Mikäli laminaatti on symmetrinen, proseduuri yksinkertaistuu, koska symmetriselle laminaatille kytkentämatriisi [B] = 0. Mikäli symmetriseen laminaattiin kohdistuva kuorma sisältää vain tasokomponentteja, riittää tasojäykkyys- ja -tasojoustomatriisien laskenta. Kaikkien kerrosten venymät laminaattikoordinaatistossa ovat tässä tapauksessa yhtä suuret. Kun symmetriseen laminaattiin kohdistuu puhdas taivutuskuormitus, lasketaan vastaavasti vain taivutusjäykkyys- ja taivutusjoustomatriisit. Kerrosvenymät laminaattikoordinaatistossa muuttuvat tässä tapauksessa lineaarisesti kerroksen paksuuden läpi.

Laskenta monimutkaistuu jossain määrin, kun laminaattiin kohdistuu sisäisiä kuormia, toisin sanoen kun laminaatti ja sen kerrokset kokevat kuvan (8.14) mukaisia lämpötila- ja kosteusmuodonmuutoksia. Kun lämpötila-/kosteusmuutos oletetaan samaksi koko laminaatissa, laskentaproseduuri on seuraava:

1. Lasketaan laminaatin jäykkyysmatriisit [A], [B] ja [D] kaavoilla (8.53), (8.63) ja (8.71) ja näistä edelleen joustomatriisit [a], [b] ja [d] kaavoilla (8.75).

• Lasketaan lämpötila- ja kosteusmuutoksia vastaavat ekvivalentit voimat ja momentit kaavoilla (8.82) ja edelleen näennäiset voimat ja momentit kaavalla (8.84).

• Ratkaistaan kaavasta (8.84) laminaatin keskitason venymät ja käyristymät:

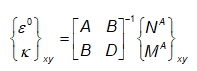
                                                                      (8.94)

• Lasketaan laminaatin keskitason venymistä ja käyristymistä tarkasteltavan kerroksen todelliset venymät laminaattikoordinaatistossa kaavalla (8.45).

• Lasketaan tarkasteltavan kerroksen todelliset venymät kerroskoordinaatistossa muunnoskaavalla (8.29).

• Lasketaan tarkasteltavan kerroksen jännitykset kerroskoordinaatistossa ottaen huomioon, että kerroksen vapaa lämpö- ja kosteuslaajeneminen ei aiheuta jännityksiä:

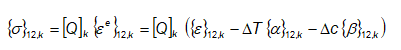
                    (8.95)

Haluttaessa voidaan myös laskea kerroksen jäännösvenymät soveltaen kaavaa (8.92) kerroskoordinaatistossa. Jännitykset ja venymät laminaattikoordinaatistossa saadaan muunnoskaavoilla (8.31).

Edellä kuvattu tarkastelu on melko suoraviivaisesti laajennettavissa kattamaan myös tapaukset, joissa lämpötilan ja/tai kosteuden muutos on z-koordinaatin funktio.

8.3.9 Klassisen laminaattiteorian käytettävyys

Klassinen laminaattiteoria kuvaa varsin tarkasti jatkuvan laminaatin käyttäytymisen niin kauan kuin kappaleen 8.3 alussa esitetyt oletukset ovat voimassa. Malli kuvaa suhteellisen hyvin melko paksujenkin laminaattien käyttäytymisen. Mallia voidaankin käyttää useiden senttimetrien paksuisten laminaattien analysointiin erityisesti, kun laminaattiin kohdistuu vain tasokuormitus.

Luvun 6 mukaisesti oletus lineaariselastisesti käyttäytyvistä kerroksista on myös useimmiten voimassa riittävällä tarkkuudella, kun kuormitustaso on alhainen. Matriisi- ja sidosvauriot alentavat kuitenkin kerrosten kuormankantokykyä, mikä on erityisesti havaittavissa mattolujitteisten kerrosten ja laminaattien jännitysvenymäkuvaajissa (vrt. kuva 6.23). Klassista laminaattiteoriaa voidaan tässäkin tapauksessa soveltaa suurillakin kuormituksilla esimerkiksi kuvaamalla kerrosjäykkyydet kuvan 8.15 mukaisilla, murtojännityksiin ja –venymiin perustuvilla sekanttimoduleilla. Tulosten epätarkkuus on kuitenkin pidettävä mielessä.

Kuva 8.15 Tangentti- ja sekanttimodulien määrittelemät jännitysvenymävastaavuudet.

Klassisen laminaattiteorian ehkä suurin puute on se, että se ei ota huomioon tasoa vastaan kohtisuorien leikkausvoimien aiheuttamia jännityksiä ja muodonmuutoksia. Nämä ovat merkityksellisiä erityisesti paksujen laminaattien taivutuskuormituksessa. Laminaattiteorian pohjalta onkin kehitetty malleja, joilla tasoa vastaan kohtisuorien leikkausvoimien vaikutukset voidaan ottaa huomioon. Mallit jätetään tässä yhteydessä tarkastelun ulkopuolelle. Yhteenveto malleista on esitetty mm. lähteessä [7].

Klassinen laminaattiteoria ei myöskään kuvaa oikein jännitystilaa laminaatin vapaan reunan läheisyydessä, johon kerrosten erilaisen käyttäytymisen takia syntyy merkittäviä tasoa vastaan kohtisuoria normaali- ja leikkausjännityksiä (kuva 8.16). Jännitysten suunta ja suuruus riippuvat laminaattirakenteesta ja laminaatin kuormituksesta. Alue, jossa jännitykset ovat merkittäviä, on leveydeltään likimain kaksi kertaa laminaatin paksuus. Jännityksiä voidaan joissakin erikoistapauksissa arvioida analyyttisesti. Pääasiassa nämä ”vapaan reunan jännitykset” määritetään kuitenkin numeerisesti elementtimenetelmällä. Määritysmenetelmät jätetään tässä yhteydessä tarkastelun ulkopuolelle. Yhteenveto vapaan reunan jännityksistä ja niiden määritysmenetelmistä on esitetty mm. lähteessä [8].

Kuva 8.16 Jännitystila laminaatin vapaan reunan läheisyydessä.